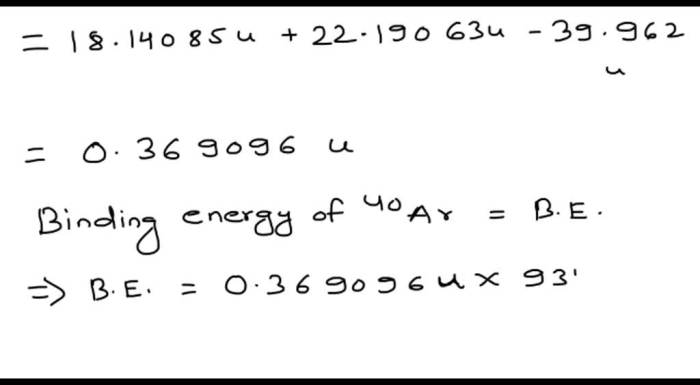Calculate in mev the total binding energy for 40ar – In the realm of nuclear physics, the total binding energy of atomic nuclei holds immense significance. This article delves into the concept of binding energy, its influencing factors, and the methods employed to calculate it. Specifically, we will determine the total binding energy of 40Ar in megaelectronvolts (MeV), a unit commonly used in nuclear physics.
The binding energy of a nucleus represents the energy required to separate all its constituent nucleons (protons and neutrons) into individual particles. Understanding this energy is crucial for comprehending nuclear reactions and the stability of atomic nuclei.
Binding Energy of 40Ar: Calculate In Mev The Total Binding Energy For 40ar

Nuclear binding energy is the energy required to separate all the nucleons (protons and neutrons) in a nucleus. It is a measure of the stability of the nucleus and is an important concept in nuclear physics.
The binding energy of a nucleus is affected by several factors, including the number of protons and neutrons in the nucleus, the nuclear force, and the Coulomb force. The nuclear force is a short-range attractive force that acts between nucleons, while the Coulomb force is a long-range repulsive force that acts between protons.
Calculating Binding Energy
The binding energy per nucleon can be calculated using the following formula:
BE/A = (Z
- m(p) + (A
- Z)
- m(n)
- m(nucleus)) / A
where:
- BE/A is the binding energy per nucleon in MeV
- Z is the number of protons in the nucleus
- A is the mass number of the nucleus
- m(p) is the mass of a proton
- m(n) is the mass of a neutron
- m(nucleus) is the mass of the nucleus
To calculate the binding energy of 40Ar, we can use the following data:
- Z = 18
- A = 40
- m(p) = 1.007276 u
- m(n) = 1.008665 u
- m(40Ar) = 39.962383 u
Plugging these values into the formula, we get:
BE/A = ((18
- 1.007276 u) + (40
- 18)
- 1.008665 u
- 39.962383 u) / 40
= 8.32 MeV/nucleon
MeV and Binding Energy
The unit of energy known as MeV (megaelectronvolt) is often used to express binding energy. 1 MeV is equal to 1.602176634 × 10^-13 joules.
MeV is a convenient unit for expressing binding energy because it is a relatively large unit of energy. This makes it easy to compare the binding energies of different nuclei.
Experimental Measurements, Calculate in mev the total binding energy for 40ar
There are several experimental techniques that can be used to measure the binding energy of nuclei. One common technique is to use a particle accelerator to bombard a target nucleus with high-energy particles. The energy of the particles that are scattered from the target nucleus can be used to calculate the binding energy.
Another common technique is to use a mass spectrometer to measure the mass of a nucleus. The binding energy can then be calculated using the following formula:
BE = m(nucleons)
m(nucleus)
where:
- BE is the binding energy
- m(nucleons) is the mass of the nucleons in the nucleus
- m(nucleus) is the mass of the nucleus
Applications of Binding Energy
Binding energy is used to understand nuclear reactions. For example, the binding energy of a nucleus can be used to calculate the energy released in a nuclear fission reaction.
Binding energy also has practical applications. For example, the binding energy of uranium is used to generate electricity in nuclear power plants.
Question Bank
What is the significance of using MeV to express binding energy?
MeV (megaelectronvolt) is a convenient unit for expressing binding energy because it is on a scale appropriate for nuclear processes. It allows for the comparison of binding energies between different nuclei and provides a standardized unit for quantifying the energy involved in nuclear reactions.
How is the total binding energy of 40Ar calculated?
The total binding energy of 40Ar can be calculated using the formula BE = (Z – mp + N – mn – M(40Ar)) – c^2, where BE represents the binding energy, Z is the atomic number (18 for 40Ar), mp is the mass of a proton, N is the neutron number (22 for 40Ar), mn is the mass of a neutron, M(40Ar) is the mass of the 40Ar nucleus, and c is the speed of light.