Determine whether the following graph can represent a normal curve – Whether a graph can represent a normal curve is a crucial question in statistics. The normal distribution, also known as the bell curve, is a fundamental concept that models the distribution of many real-world phenomena. This article will explore the characteristics of a normal curve, provide methods to visually inspect a graph for normality, and discuss statistical tests to formally determine its adherence to the normal distribution.
Introduction to Normal Curves

A normal curve, also known as a Gaussian distribution, is a bell-shaped curve that describes the distribution of a random variable whose values are normally distributed. It is a continuous probability distribution that is symmetric around its mean, with the highest point at the mean and decreasing values as you move away from the mean.
Normal curves are found in many real-world phenomena, including the distribution of heights in a population, the distribution of test scores, and the distribution of errors in measurements.
Characteristics of a Normal Curve: Determine Whether The Following Graph Can Represent A Normal Curve
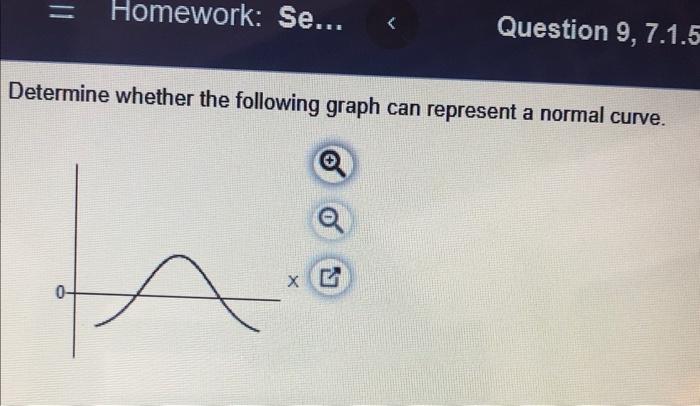
Normal curves have several key characteristics:
- Bell-shaped:The curve is bell-shaped, with the highest point at the mean and decreasing values as you move away from the mean.
- Symmetric:The curve is symmetric around its mean, meaning that the left and right halves of the curve are mirror images of each other.
- Mean, median, and mode:The mean, median, and mode of a normal curve are all equal.
| Measure | Definition | Relationship |
|---|---|---|
| Mean | The average value of the data | Equal for a normal distribution |
| Median | The middle value of the data | |
| Mode | The most frequently occurring value in the data |
Analyzing the Graph
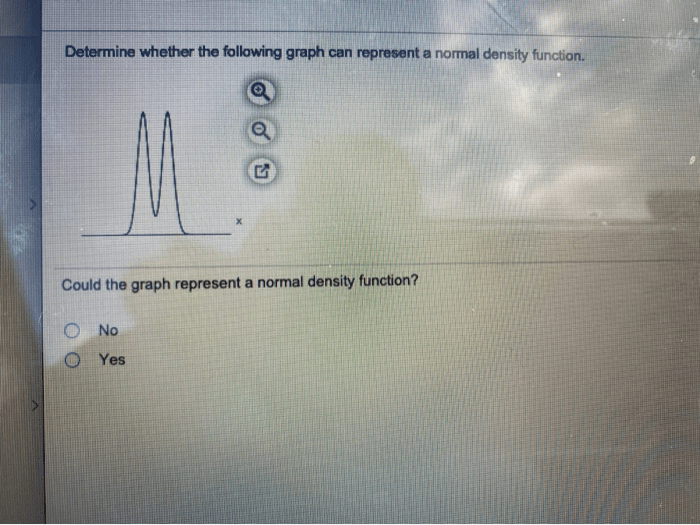
To determine if a graph represents a normal curve, you can visually inspect the shape, symmetry, and spread of the data points. If the data points are bell-shaped, symmetric, and have a similar spread, then it is likely that the data is normally distributed.
Here are some specific things to look for:
- Shape:The curve should be bell-shaped, with the highest point at the mean and decreasing values as you move away from the mean.
- Symmetry:The curve should be symmetric around its mean, meaning that the left and right halves of the curve are mirror images of each other.
- Spread:The spread of the data points should be similar. If the data points are too spread out or too clustered, then it is less likely that the data is normally distributed.
Statistical Tests
In addition to visual inspection, there are also statistical tests that can be used to formally determine whether a graph represents a normal curve.
Two common statistical tests for normality are the Shapiro-Wilk test and the Kolmogorov-Smirnov test. These tests compare the distribution of the data to a normal distribution and return a p-value. If the p-value is less than 0.05, then it is likely that the data is not normally distributed.
Applications
The analysis of normal curves is used in a variety of fields, including:
- Statistics:Normal curves are used to model the distribution of random variables and to make inferences about populations.
- Finance:Normal curves are used to model the distribution of stock prices and other financial data.
- Quality control:Normal curves are used to monitor the quality of products and processes.
Essential FAQs
What is the significance of a normal curve?
The normal curve is a fundamental statistical model that represents the distribution of many natural and social phenomena. It is characterized by its bell shape, symmetry, and specific mathematical properties, making it a useful tool for describing and predicting the distribution of data.
How can I visually assess the normality of a graph?
Visual inspection of a graph can provide insights into its normality. Look for a bell-shaped curve that is symmetric around the mean. The data points should be evenly distributed on both sides of the center, without significant skewness or outliers.
What statistical tests can be used to formally determine normality?
Statistical tests, such as the Shapiro-Wilk test and the Kolmogorov-Smirnov test, can be used to formally assess the normality of a dataset. These tests compare the distribution of the data to the expected distribution of a normal curve and provide a statistical measure of the difference.